Correlating Education Course(s) to Value

I would work on getting an average recognition index per course, together with an "inverse" course take-up score.
The problem is that particular course take-up could be a function of number of courses taken since those perceived as harder may not be taken up.

Okay, good idea. In this fictional scenario, the recognition index is only attributable to the employee overall. There's no explicit/implicit linkage of any single course (or courses) to the recognition index - so that's why I think this problem will lend itself to an inference solution, based on the pattern of the data (courses taken correlated to the recognition index).

At first blush (quick reading) it looks like it may be a linear or logistic regression problem (relationship between the number of courses and the recognition index). Then, try a factor analysis with each course as a factor to find key courses that influence the overall recognition index.

Okay, a friend here at work also suggested that a "cluster analysis" (which is the equivalent of the factor analysis) might be one statistical technique to use, since it's a non-parametric test.

I had speculated that the other solution might be a multiple regression (linear) solution, similar to what JPB has suggested. Does that sound about right?

I'll concede that I'm in uncharted territory with both the factor analysis and the multiple regression (I can mastermind the regression of one variable . . .), and any help on setting up the problem equation for either of those would be a big help. Thanks!

I was looking back at some past postings and I saw this, so I thought I would try and "close the loop" - maybe for the benefit of others down the road, who encounter a similar situation, especially since some of this feedback did help me get going in the right direction. although I did have to reach out to some of our staff PhDs for a little more help (although I can't understand but about half of what they say, most of the time . . .).

So, a multiple regression strategy turned out to be the approach to use, to bring this effort to ground. First, I used multiple regression to ascertain whether there was simply any optimal number of courses that contributed (or failed to contribute) to increases in the Recognition Index.

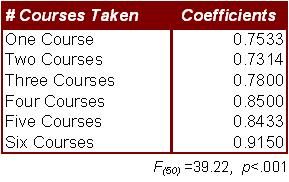
That proved not to be the case, as any additional course taken appeared to be positively correlated with a higher Recognition Index value.

Next, using multiple regression again, I looked at whether any specific courses taken could predict a higher Recognition Index. Luckily, in my fictional example, it was assumed that the courses listed were not taken in any predetermined order, and without any requirements for any prior course prerequisites.

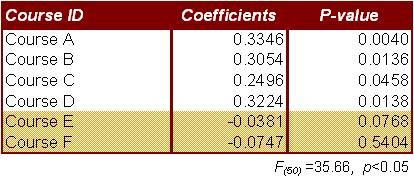
This showed which independent variables (Course #s) were the least significant (relative to the level of significance selected), and which did not substantially predict increases in the Recognition Index.

This gave at least an empirical evidence and basis for which courses the organizations (and the employees) would optimally benefit from, especially if budgets "got tight", at some point in the future.


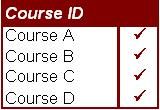
Since all of these analyses, seemingly beget another round of analysis, if the information were available, the next logical examination would likely include an analysis of the specific order in which the courses were taken. And in the spirit of full disclosure (in case someone is so motivated as to start "checking" my answers here on a slow Sunday [or ever in the future]), my fictional case study actually contained 50 "cases", but I only populated 10 cases for this posting, mostly to provide some "data direction" and help the collective audience understand where this might need to go.

This was a good posting, and a fun (okay, reasonably fun) task. Thanks for the help.