1vs2 70% success. Calculate choice over pool data of 90% or better

Personally, I think it would be good to stop before someone hit me.

If it's hard to understand I am trying to go with a memory retention question let's say it's tiles and you flip them so it's a 1 or 2 underneath so 50/50 but you gotta see for a moment so you more have 70 percent chance. Scrub the fact you should remember for certain by the second or third attempt. But at the end of 10 attempts you can look at your answers and you see 2 2s and 8 1s it would be what percent effective to go with 1 over 2 as your answer and it is greater then 70 percent at that point. I just want to know how many attempts to get it to a 90 percent effectiveness for a tabletop game custom content. And each attempt takes time from the player to make it more fair.

So after 10 rolls of a 1d10 giving them 70 percent odds and them choosing 1 vs 2 at the end of their attempts looking at the pool of success vs loses and them obviusly choosing the hogher outcome what die would I roll and what numbers of success would I give the player. Keeping with actual numbers of probability versus just the actual outcome of their particular rolls.

One roll of the dice has absolutely no influence on any following rolls. Your chances remain the same no matter how often you roll them.

Im sorry your not understanding I do have difficulties due to my autism I supose articulating. So let's put it this way you have a weighted coin with 70 percent chance it lands on one side 30 percent on the other let's forget about the rim of the coin. So you are trying to flip the coin enough to be 90 percent sure which side of the coin is the 70 percent side

I understood the situation. My reply is correct.

Sure but it doesn't address the question at all.
Given a million tosses you will see 70 percent and can 100 percent certain or 99.9999 percent certain say which side of the coin is the 70 percent one your just not grasping the question it's Otay;)

The question is simply how many tosses to get to 90 percent certain of which side of the weighted coin would be the one that comes up 70 percent of the time because one isn't enough nor 2 nor 3 20 should be close 100 would be probably 98 percent or so certain whichever side comes up more often is the 70 percent one not the 30 it should be a simple concept but hey its Otay as I said

set.seed(17) # Today's date.
coin.power = function(ntoss=100,nsim=1000,prob=.5){
lower = qbinom(.025,ntoss,.5)
upper = qbinom(.975,ntoss,.5)
rr = rbinom(nsim,ntoss,prob)
sum(rr < lower | rr > upper) / nsim
}
ntosses = c(10,100,200,500,600,800,1000,1500,2000,2500)
res = sapply(ntosses, coin.power, prob=.55)
names(res) = ntosses
res
10 100 200 500 600 800 1000 1500 2000 2500
0.032 0.133 0.259 0.634 0.653 0.799 0.867 0.969 0.994 0.999
In the case of a coin with a true biased probability of heads of P(H)=55%
, then, you can expect to reject correctly the hypothesis that the coin is fair 99.4%
of the times if you toss the coin 2,000
times, and 96.9%
of the times with 1,500
tosses.

If the coin is more biased, for example, P(H)=70%
, you can expect virtual certainty with 200
tosses

https://www.calculator.net/sample-size-calculator.html?type=1&cl=90&ci=3&pp=70&ps=&x=66&y=19



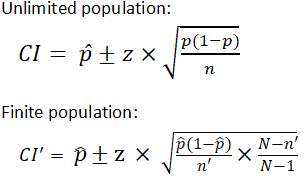
A sample size of 229 with 90% confidence, sample error of 5% and a sample mean of 0.70.

If the question is "you know you have a biased coin that comes up either heads or tails 70% of the time, but you don't know which and you want to flip it until you have a 90% confidence that you can say whether the coin is favored to heads or tails, you need nine flips. Lets say heads is more favored. After nine flips, you have a 90.2% chance of having 5 or more heads, so if you knew the coin was biased, you could say it is biased towards heads with a 90% confidence.

Here is the breakdown
Nine heads 4%
Eight heads 16%
Seven heads 27%
Six heads 27%
Five heads 17%