NeoPets Riddles (Lenny Conundrums) and Answers Here

no, that will give you an approximation but not the exact

ah, i thought as much. thanks.

In calculus, one learns that velocity is the integral of acceleration, and position is the integral of velocity. Since the acceleration function is piecewise in this case, it is helpful to work on each interval separately.

For 0 < t < 15, the acceleration is given as being a(t) = 2t. Then the velocity function is v(t) = t^2 + v(0) = t^2, and the position function is s(t) = (1/3) t^3 + s(0) = (1/3) t^3. Then the distance covered on this interval is s(15) = (1/3)(3375) = 1125 m, with the velocity at t = 15 being v(15) = 225 m/s and the acceleration being a(15) = 30 m/s^2.

For the thirty-second interval, restart the time at t = 0, so we're looking at 0 < t < 30. On this interval, the acceleration is given as being constant, so a(t) = 30 m/s^2 on the interval. The velocity had already increased from zero (at the start) to 225 m/s, and we are now adding to that, so v(t) = 30 t + 225, with the velocity at the end of this interval being v(30) = 1 125 m/s. The position on this interval is given by s(t) = 15 t^2 + 225 t, with the position at the end of the interval being an additional s(30) = 15 (30)^2 + 225 (30) = 20 250 m.

For the final fifteen-second interval, restart the time again at t = 0, so we're looking at 0 < t < 15. Since acceleration is zero on this interval, then the velocity is constant, being the velocity at the end of the previous interval: v(t) = 1 125. Then the position is given by s(t) = 1 125 t, and the position at the end of this interval is an additional s(15) = 1 125(15) = 16 875 m.

Adding, we have 1 125 + 20 250 + 16 875 = 38 250 m.

Note: The question asks "how far did the ship travel after one minute?" How far the ship went after that first minute is unknowable. I would guess that they meant to ask "how far had the ship travelled in that first minute?"

Eliz.

ok My mind is officially blown!

These ones are way beyond my control. I didn't take calculus. My daughter is taking Calculus in college right now in college & about to pull her hair out!

She made her first B ever when she encountered calculus for the first time! She made an 89, then came calculus 2, same thing, now she is in calculus 3 & she might make an A in this one! She is working her butt off.

As for Lenny, I haven't a clue, I was lost at the ship went this fast in the first so many seconds... blah blah blah. Now the past two weeks I figured those out.

So some nice souls out there, I'm going to need a little help with this one if you please.... I am not a math person

I agree with this: the velocity, as someone said on far previous pages, should be 240m/s at the end point of the 15th second. And the distance during the first 15 seconds is 1240m.
So, I'm afraid the answer of 38250m should NOT be right??

Kindly provide your work and reasoning. Please be complete. Thank you.

Eliz.

I think it should goes link this...



http://picasaweb.google.com/illume.admail/LennyConundrums/photo#5184849970342751330

therefore, the total distance is about 28xxx

See these links below:

Webpage Title
This guy got the right 15th second's velocity (240m/s) and right distance during those 15 seconds (1240m).
However, the later work was wrong because the middle 30 seconds should still be accelerated, where a=30.
Only the last 15 seconds keeping in the same speed, where v=240*30+30*30...

Alternatively, check this work:
Webpage Title
using Excel calculated the right 15th second's velocity (240m/s) and a=30.
However, the distance was wrong.

If the velocity at the 15th second WAS 240m/s, and the distance during those 15 seconds WAS 1240m, I believe we all know how to continue the next steps.

Actually you cannot use those equations... Those kinematic equations are for CONSTANT acceleration ONLY... Thus for the first part where acceleration is increasing, I suggest to find the equation of the line, which is a quadratic curve, then integrate the equation using the limits of t=0 to t=15. Then you should get your result for distance.

The rest is pretty simple... For the 2nd phase you use the kinematic expressions and for the last phase you just find the velocity at t=30 and multiply that by 30s and you will obtain total distance travelled in the last phase. Then add the 3 components together to get your final result.

Edit: I'm not too sure whether Excel has the capability to integrate line functions but I manually did the integration... Its a really simple integration so I think you guys can easily solve it!

ANSWER
i think i got the answer.
well it says that for the first 15sec at each sec the acceleration increases by 2m/s^2. so that means that time=0 a=0
then time=1 a=2. time=2 a=4, time=3 a=6, and so on till time =15sec so a=30m/s^2. what needs to do with this information is that they need to find out how far the ship traveled each of those seconds. but befor u can do that u need the speed at each second. so ween to calculate speed. we will use the following formula of velocity as a funtion of time
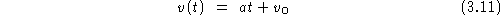
so for the time =1 we plug in a=2, t=1, and Vo=0 and we get v at 1second to be 2m/s we do this again but this time a=4 Vo=2 t=1(we are working with indivisual seconds) and we get v at 2seconds to be 5m/s. so the total velocity at 2 seconds is 5m/s not 5+1=6. we continue to do this for the first 15sec. i suggest u write down each indivisual velocity seeing that u will need them later on in the calculations. so the velocitry if u did this correctly should 239m/s at the 15 second mark. don't forget the objective of the problem we need the distance not spped. the way to get the distance traveled is by using the formula position as a function time and velocty. X=Xo+.5(Vo+V)
where x is the distance Xo is the intial distance, Vo intial velocity, and v is the velocity.
for time=0 to time=1 Vo=0 V=1 Xo=0 so x=.5
for time 1 to time=2 Vo=1 V=5 Xo=.5 so x=3.5
note the total distance is not 3.5+.5=4m( once again i say this we are ddealing with each indivisual second. so the totaldistance traveld the first 2 seconds is 3.5m
u continue this 13 more times till u reach time =15. the total distance should be 1345.5m.
this is for the first 15 seconds not the whole minute. we still have to calulate the other 45seconds now.
the problem now states that the ship goes at a constant acceleration for the next 30seconds. this means the ship with an acceleration on 30m/s^2 for 30sec. the way i got 30m/s^2 is from when we calculated the acceleration in the begining. this part is pretty easy to calculate. because the acceleration is constant we use the formula position as a funtion of time and acceleration

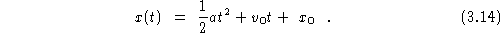
what we do is plug in Xo=1345.5 Vo= 239 t=30 and a=30
when we do this we get a value of 22015.5m this is the total distance traveled for the first 45sec. people may be wndering why i used 30 for the time instead of one, well the reason is that the acceleration is constant here and if the other part the acceleration was not constant it was increasing by 2m/s^2 everysecond. now for the third part of the problem we know that there is zero accleration, which means that the velocity is constant. to calculate the the distance traveld in the last 15seconds we need to first know the speed at which the ship is moving at. so we have to calculate the velocity of the ship at the 45second mark. we do that with the following formula position as a function time and velocty. X=Xo+.5(Vo+V) this formula can only be used when there is a constant acceleration which there is for the 30secs.
we plug in x=22015.5 Xo=1345.5 Vo= 239 and t=30
from this we get v= 1139m/s
we then take that velocity and plug it into the formula position as a funtion of time and accleration
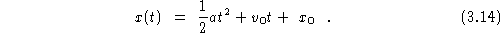
we plug Xo=22015.5 Vo=1139 t=15 and a=0 and solve for x.
as a result u should get the total distance traveld by the ship to be 39100.5m in the first minute(60sec). that is the number u put into the lenny conundrum

i forgot one thing, the answer has to be a whole number not a deicmal answer. it says to round to the nearst whole number. i say round down to 39100m because if u round up to 39101 u r saying that the ship traveled the extra .5m when it didnt. but by saying 39100 it says for sure it traveled the 39100m plus a little extra but not enough to count.

it may look nicer to round lower, but when the decimal is .5 or larger, you're supposed to round up, so wouldn't that be it?

i was not trying to make it look nice. the reason i said 39100 instead of 39101 is because the ship did not travel 39101m, but it did travel 39100m in the first minute. that is what i was trying to say.

sorry but i dont know a thing about calculus

It says in the LC "nearest whole number," and the convention when it's .5 is to round up. I've asked if they can't specify ALWAYS ROUND UP to take out the ambiguity, but it's hit or miss with this kind of thing. [I'm sore because I missed that awful "obscure units of measurement" one because I rounded down and not up because the reference I found was slightly different... *shakes fist*]

the rule with .5 rounding is that if the number befor it is an even number u round down, but if if the number is odd then u round up. I learned that in school sometime back. i have stuck with it for some time now and it has not failed me yet. Also, this is not calculus. This is classical physics. i just learned this stuff last semester.

Actually, this is not "the" rule for rounding; it is "a" rule, and not the most-common one. "Banker's rounding" is generally used in finance and statistics. Sorry.


Actually, it is highly unlikely that any physical object would move in this step-wise sort of fashion, so the step-wise function your post implies would not seem sensibly to apply to this situation. As such, it would appear that your numerical values are at least somewhat suspect. Sorry.


Actually, Isaac Newton invented the calculus in order to invent classical physics. The two are fairly-well intertwined -- though very elementary physics courses may not require calculus. The physics equations of motion are derived by using the calculus, as shown in previous posts. Sorry.

Eliz.

Note: If, some day, you take calculus, you will then learn that what you have done is a sort-of approximation to the integration necessary to find the answer; specifically, you have approximated the "right-hand endpoint" form of the Riemann sum, using uniform subintervals.

You are right! Calculus has to be used to do the first part's culculation, so at the 15th seconds, v=225m/s. I know you are a good math man:)

You people who are claiming that this doesn't require calculus have no idea what thrust is, and probably already got the answer wrong.

Sorry.

hi guys I am new. why hasn't the lc started for this week.. it usually starts a few hours ago...