Hafele and Keating Experiment
"During October, 1971, four cesium atomic beam clocks were flown on regularly scheduled commercial jet flights around the world twice, once eastward and once westward, to test Einstein's theory of relativity with macroscopic clocks. From the actual flight paths of each trip, the theory predicted that the flying clocks, compared with reference clocks at the U.S. Naval Observatory, should have lost 40+/-23 nanoseconds during the eastward trip and should have gained 275+/-21 nanoseconds during the westward trip ... Relative to the atomic time scale of the U.S. Naval Observatory, the flying clocks lost 59+/-10 nanoseconds during the eastward trip and gained 273+/-7 nanosecond during the westward trip, where the errors are the corresponding standard deviations. These results provide an unambiguous empirical resolution of the famous clock "paradox" with macroscopic clocks."
J.C. Hafele and R. E. Keating, Science 177, 166 (1972)
Around the World
In 1971, experimenters from the U.S. Naval Observatory undertook an experiment to test time dilation . They made airline flights around the world in both directions, each circuit taking about three days. They carried with them four cesium beam atomic clocks. When they returned and compared their clocks with the clock of the Observatory in Washington, D.C., they had gained about 0.15 microseconds compared to the ground based clock.
Eastward Journey Westward Journey
Predicted -40 +/- 23 ns + 275 +/- 21 ns
Measured -59 +/- 10 ns + 273 +/- 7 ns
Around-the-World Atomic Clocks
In October 1971, Hafele and Keating flew cesium beam atomic clocks around the world twice on regularly scheduled commercial airline flights, once to the East and once to the West. In this experiment, both gravitational time dilation and kinematic time dilation are significant - and are in fact of comparable magnitude. Their predicted and measured time dilation effects were as follows:
Predicted: Time difference in ns
Eastward Westward
Gravitational 144 +/- 14 179 +/- 18
Kinematic -184 +/- 18 96 +/- 10
Net effect -40 +/- 23 275 +/- 21
Observed: -59 +/- 10 273 +/- 21
Gravitational calculation Kinematic calculation
Gravitational Time Shifts
For small changes in gravitational field associated with changes in altitude above the earth, the approximate time dilation expression is
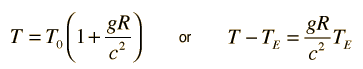
if a comparison is made between a clock on the Earth's surface (TE) and one at height h above the surface (T). Hafele and Keating predicted a time difference of 144 ns on an eastward flight around the world for which the flight time was 41.2 hours. This corresponds to an average height of 8900 m, a reasonable flight altitude for a commercial airline. The time shift is positive (aging faster) for both eastward and westward flights. The predicted value of 179 ns for the westward flight of 48.6 hours duration corresponds to an average altitude of about 9400 meters.
Kinematic Time Shift Calculation
If the kinematic time dilation expression
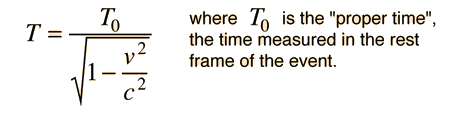
is expanded in a binomial expansion, then for small velocities it becomes
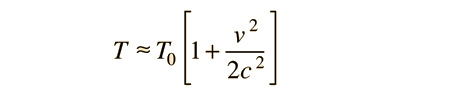
This expression can be used to compute the time dilation in the Hafele-Keating experiment in which an atomic clock was taken aboard an aircraft and compared to a ground-based closk. The problem encountered with measuring the difference between a surface clock and one on an aircraft is that neither location is really an inertial frame. If we take the center of the earth as an approximation to an inertial frame, then we can compute the difference between a surface clock and the aircraft clock. Taking a "proper time" at the earth's center as if the master clock were there, the time measured by a clock on the surface would be larger
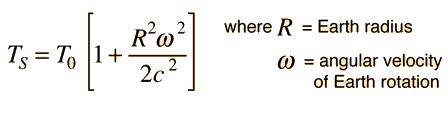
and that for the airborne clock would be approximately
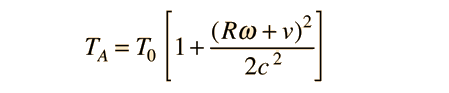
since to the level of the approximations used, the height of the aircraft does not significantly change the radius R. The difference in the times compared to our hypothetical master clock would then be
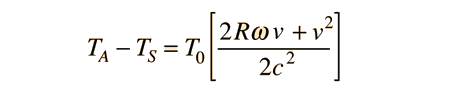
Now this relationship is just the reverse of the actual experiment, since we have assumed that the clock is at the center of the earth, whereas the actual clocks are in the frames which are moving with respect to the center. The time difference expression should be valid, but in comparing the aircraft clock to the surface clock, we should find that it has fallen behind, so we can model that time difference by

Note that the "earth center" time has been replaced by the surface time in this expression. This is a valid approximation in this case since the time difference is many orders of magnitude smaller than the time itself, and this allows us to model the difference between two measurable times.
Aircraft Time Dilation
For an aircraft flying over the equator, its clocks will show a time shift relative to a fixed surface clock which can be approximately modeled by the expression

where the subscripts A and S refer to the aircraft and surface clocks. For travel eastward, v has a positive sign and the shift will be negative (aging more slowly). But for a westward flight the time shift is positive (aging faster) for the aircraft speeds involved. Hafele and Keating predicted time shifts of -184 ns for an eastward flight around the world and a shift of +96 for a westward flight.
If you plug in numbers for a 48 hour round trip flight at constant speed at the equator, you get -260 ns and 156 ns for the eastbound and westbound flights respectively. The predicted values obtained by Hafele and Keating presumably were based upon detailed measurements of the speeds, etc.
Hafele and Keating are credited with an experimental measurement which confirms time dilation and matches predictions with an accuracy of about 10%. It gives an experimental answer to the twin paradox.